فائدة الأعداد المركبة

الأعداد المركبة هي مفهوم رياضي أساسي يوسع نظام الأرقام إلى ما بعد الأعداد الحقيقية، وتلعب الأعداد المركبة دورًا مهمًا في مختلف فروع الرياضيات والفيزياء والهندسة وغيرها من المجالات، وفي هذه المقالة سوف نتعمق في أساسيات الأعداد المركبة وتمثيلها وعملياتها وتطبيقاتها.

تعريف الأعداد المركبة

الأعداد المركبة هي أرقام على شكل a + bi ، حيث "a" و "b" أرقام حقيقية و"i" تمثل وحدة خيالية، والتي تُعرّف على أنها الجذر التربيعي لـ(-1)، ويُشار إلى الجزء الحقيقي من العدد المركب بـ "

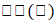
" والجزء الخيالي بواسطة "

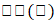
"، وتتبع الوحدة الخيالية "i" الخاصية i² = -1.

يمكن تمثيل الأرقام المركبة هندسيًا في مستوى ثنائي الأبعاد يُعرف بالمحور المركب، وفي حين يمثل المحور الحقيقي الأعداد الحقيقية، فإن المحور المركب يمثل مضاعفات الوحدة الخيالية، ويتوافق موضع العدد المركب على المستوى مع أجزائه الحقيقية والخيالية.

العمليات الحسابية على الأعداد المركبة

يمكن تطبيق العديد من العمليات الحسابية على الأعداد المركبة، بما في ذلك العمليات الآتية:

• الجمع: لإضافة عددين مركبين، ما عليك سوى إضافة أجزائهما الحقيقية والأجزاء الخيالية بشكل منفصل.
• الطرح: يتبع طرح الأعداد المركبة نفس نمط الجمع، مع طرح الجزأين الحقيقي والخيالي بشكل منفصل.
• الضرب: لضرب الأعداد المركبة، استخدم خاصية التوزيع والتبسيط وفقًا لقواعد ضرب الوحدات الخيالية.
• القسمة: قسمة الأعداد المركبة تتضمن ضرب كل من البسط والمقام بمرافق المقام، للحصول على اقتران العدد المركب عن طريق تغيير علامة الجزء الخيالي منه.

تسمح هذه العمليات بالتلاعب والحساب بأرقام معقدة، مما يسهل التحليل المعقد وحل المشكلات.

المتقارن والمعامل

مرافق العدد المركب a + bi يُعطى بواسطة (a - bi)، أي أن مرافق العدد المركب هو نفس الجزء الحقيقي ولكن الإشارة معاكسة للجزء الخيالي، وينتج عن حاصل ضرب عدد مركب ومرافقه عدد حقيقي.

يُشار إلى المعامل أو القيمة المطلقة لعدد مركب بالرمز | z | وتمثل المسافة من الأصل (0، 0) إلى النقطة التي تمثل الرقم المركب على المستوى المركب، ويُحسب المعامل على أنه الجذر التربيعي لمجموع مربعي الجزأين الحقيقي والخيالي.

صيغة أويلر والتمثيل القطبي

صيغة أويلر هي نتيجة أساسية في التحليل المعقد الذي يربط بين الأعداد المركبة والأس وعلم المثلثات، وتنص على أن 

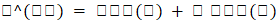
 ، حيث "e" هي قاعدة اللوغاريتم الطبيعي و"θ" هي الزاوية، وتسمح صيغة أويلر بالتعبير عن الأعداد المركبة في الصورة القطبية، حيث يمكن كتابة العدد المركب 

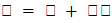
 على النحو 

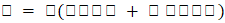
، حيث "r" هو المقياس و"θ" هي وسيطة العدد المركب.

يوفر التمثيل القطبي للأعداد المركبة تمثيلًا موجزًا يبسط العمليات الحسابية التي تتضمن الضرب والقسمة والأس.

تطبيقات الأعداد المركبة

تجد الأرقام المعقدة تطبيقات واسعة النطاق في مجالات مختلفة، بما في ذلك:

• الهندسة الكهربائية: تُستخدم الأرقام المركبة لتمثيل وتحليل دوائر التيار المتردد (AC) والمقاومة الكهربائية والطور.
• ميكانيكا الكم: تعتبر الأعداد المركبة أساسية في الصياغة الرياضية لميكانيكا الكم ، حيث تصف وظائف الموجة والاحتمالات.
• أنظمة التحكم: يتم استخدام الأرقام المعقدة في تحليل وتصميم أنظمة التحكم لنمذجة سلوك النظام وتحسينه.

تعمل الأعداد المركبة على توسيع نظام الأرقام إلى ما وراء الأعداد الحقيقية، مما يوفر قوة أداة للتحليل الرياضي وحل المشكلات، ويمكن تمثيل هذه الأعداد على المحور المركب، وهناك عدة مفاهيم أساسية تتعلق بالأعداد المركبة مثل تطبيق العمليات الحسابية، والمقارنات، والمعامل، وصيغة أويلر، والتمثيل القطبي، تمتد تطبيقات الأعداد المركبة على نطاق واسع من المجالات العلمية والهندسية، مما يدل على أهميتها في فهم الظواهر المعقدة وحلها.